Решение уравнений и система, на мой взгляд, задача более распростанённая, чем интегрирование или оптимизация. Жаль, что в некоторых программах для неё не предусмотрены специальные средства. Но у Octave с этим всё в порядке.
Если уравнение можно свести к полиному, его корни находятся с помощью функции roots(p). Вот, например, решение уравнения x^3+4*x^2-3*x+2=0.
Одиночное нелинейное уравнение может быть решено с помощью функции fzero(функция, нач.знач). В качестве начального приближения здесь может быть задана точка в окрестности корня или интервал, на котором следует проводить поиск. Функция может возвращать как найденный корень, так и значение в данной точке. В следующем примере для решения уравнения
sin(x)-x^2/4 = 0 приведены 3 способа вызова fzero().
Решение системы нелинейных уравнений ищет функция fsolve(функция, нач.знач.). Так же как и в случае fzero(), можно задать начальное приближение или интервал локализации корней. Результат может содержать только вектор корней, корни и значения, либо дополнительно параметр, характеризующий работу функции: меньше нуля - решение не найдено, 0 - достигнуто максимальное число итераций и вычисление прервано, больше нуля - решение найдено.
Впрочем, даже если программа говорит, что результат получен, лучше сделать проверку.
Уравнения, заданные в символьном виде, тоже могут быть решены. Но результат будет числовым. Для поиска корней символьных выражений используется функция symfsolve(уравнение, нач.знач.).
Данная функция позволяет также находить корни системы уравнений, но насколько удобно использовать такой символьно-числовой подход, решайте сами...



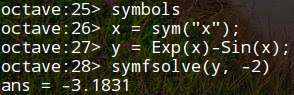
Комментариев нет:
Отправить комментарий